
Mfm2p
Factor x^{2}4x4 In general, when x^{2}bxc is a perfect square, it can always the equation must be in the form x^2BxC=0 r s = 4 rs = 4 Let r and s be the factors for the quadratic equation such that x that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxCAnswer to Write y = 4x 8 in factored form By signing up, you'll get thousands of stepbystep solutions to your homework questions You can
Y=x^2-4x-5 in factored form
Y=x^2-4x-5 in factored form-The equation is now solved 4x^ {2}2x3=y Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^ {2}bx=c 4x^ {2}2x3\left (3\right)=y\left (3\right) Add 3 to both sides of the equation(Carefulpay attention to multiplicity) Q What does multiplicity of a zero mean?

How Do You Solve A Quadratic Equation With Complex Solutions By Completing The Square Printable Summary Virtual Nerd
45 Express each equation in the specified form a y = (x – 3)² 25 in standard form B y = 2(x – 7)(x 3) in standard form C y = 2x² 28x – 26 in factored form D y = 9x² 72x 81 in vertex formAnswers 1 Get Other questions on the subject Mathematics Mathematics, 2100, deondra0803Quadratic trinomial B –5x^2 – 8x;
Algebra Factor x^24x5 x2 − 4x − 5 x 2 4 x 5 Consider the form x2 bxc x 2 b x c Find a pair of integers whose product is c c and whose sum is b b In this case, whose product is −5 5 and whose sum is −4 4 −5,1 5, 1 Write the factored form using these integersTo find the roots, consider\(\, x^29x=0\) Let's find its factored form Middle term = 9 and last term = So the numbers which give sum= 9 and product= are 4 and 5 \begin{align} x^29x&=0 \\ x^25x4x&=0\\x(x5)4(x5)&=0\\(x5)(x4)&=0\\\therefore x=5 \,or\,x&=4\end{align}We're going to take the two terms that we just factored out (x^2 and 4), and add them to get one term to multiply the "leftovers" with y = (x^2 4)(x 3) And there you have itfactored form!
Y=x^2-4x-5 in factored formのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
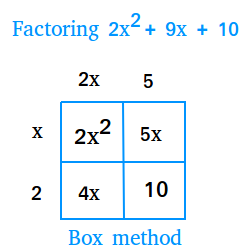
 2 | 2 |  2 |
 2 |  2 |  2 |
 2 | 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 2 | 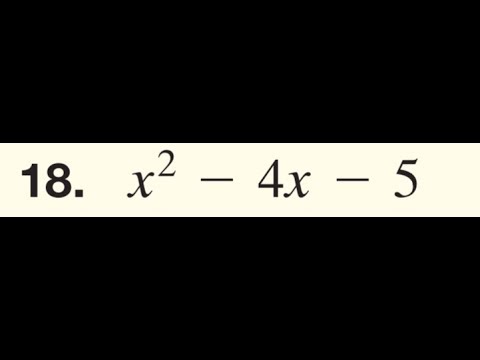 2 |
 2 | 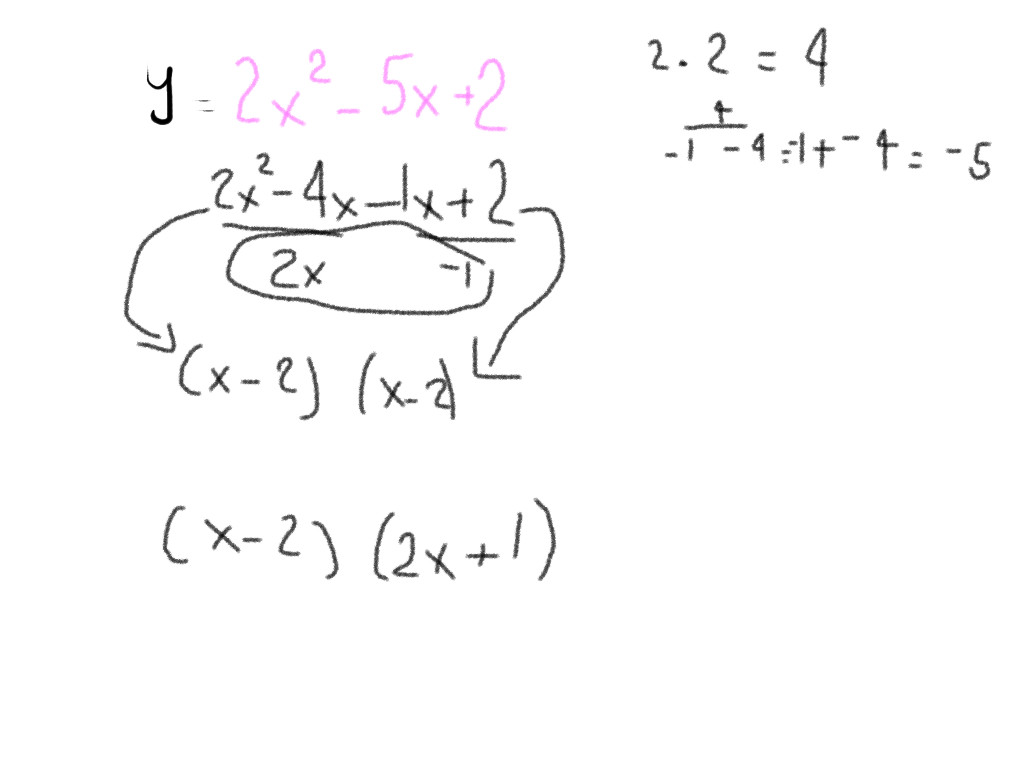 2 | 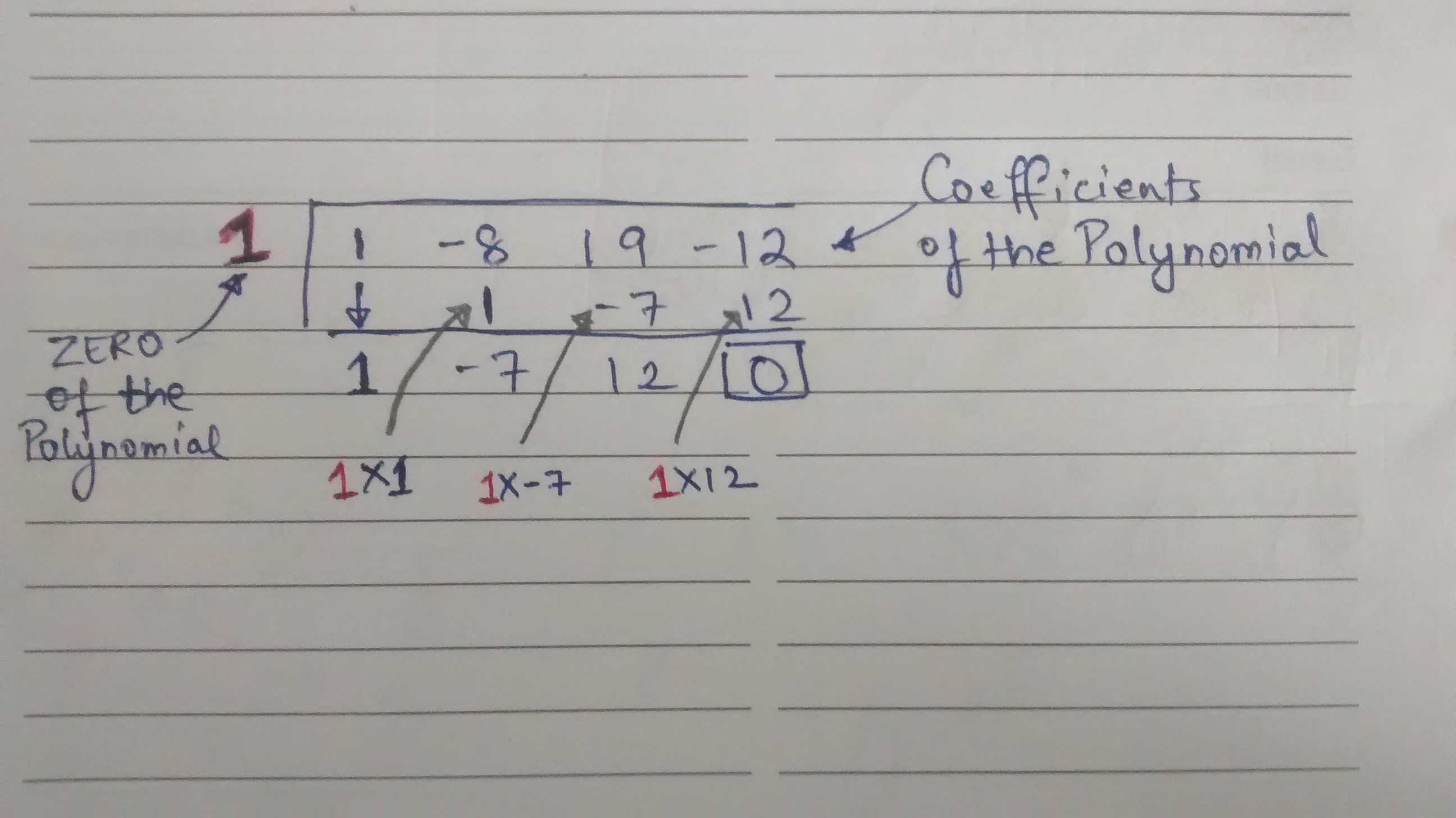 2 |
 2 |  2 | 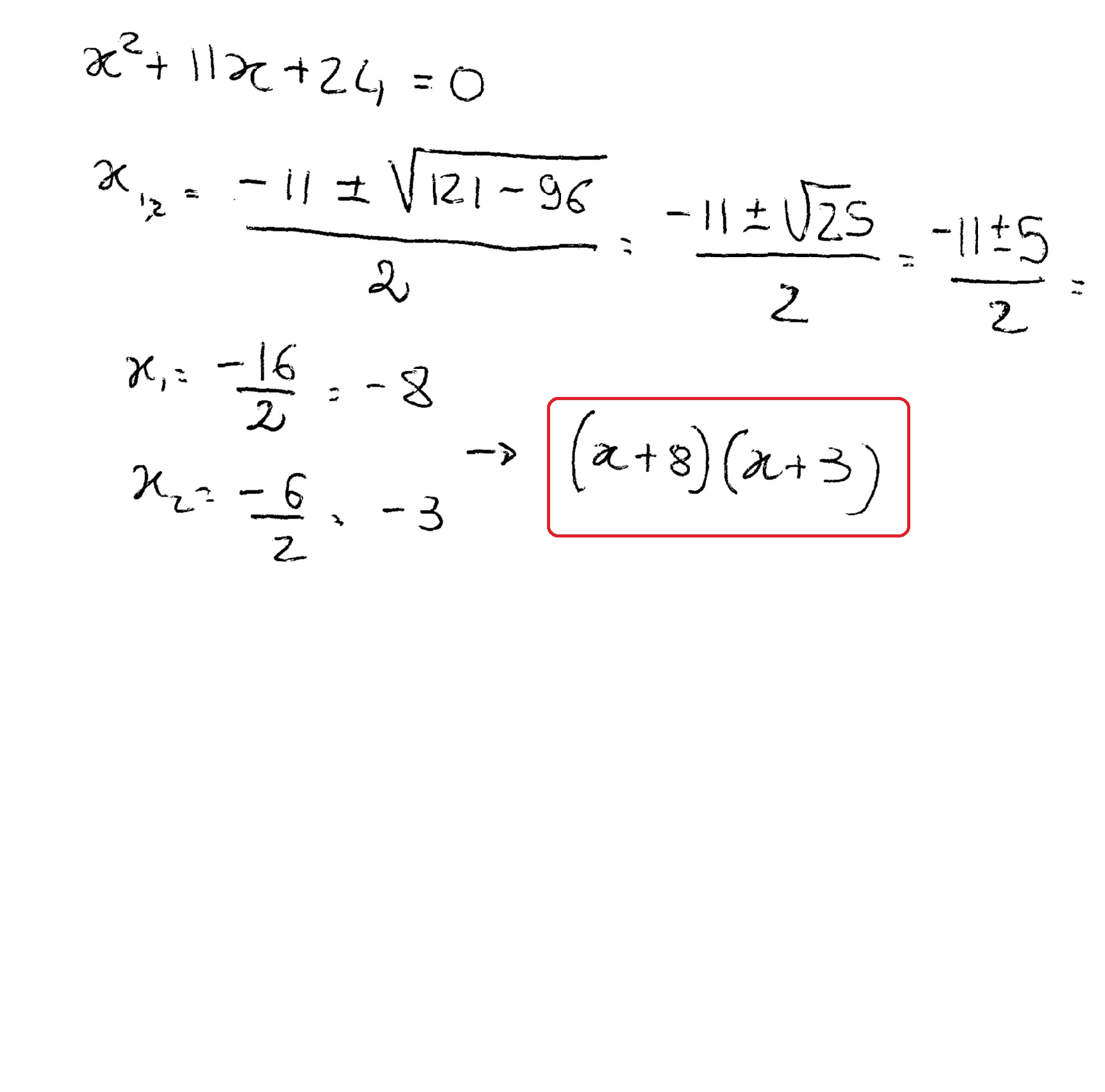 2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 | 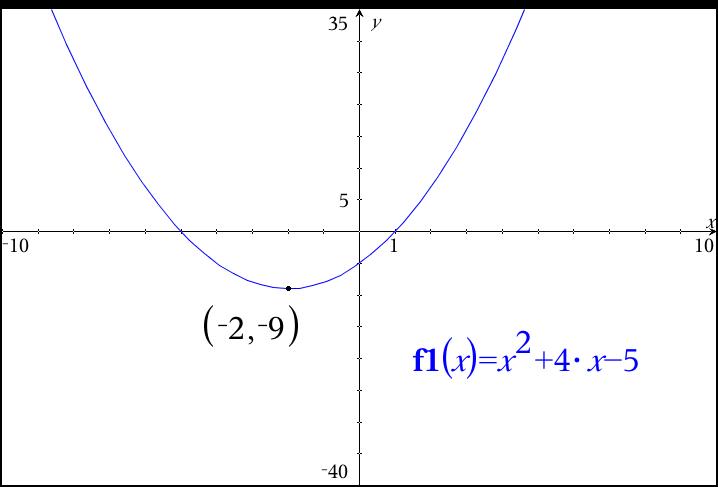 2 |
 2 | 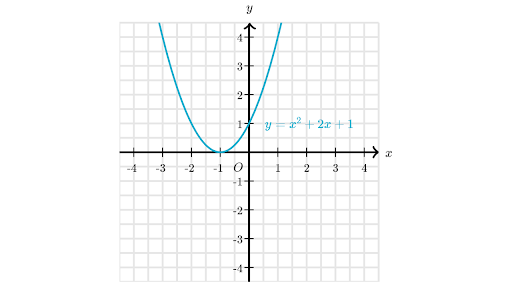 2 | 2 |
 2 | 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |  2 |
 2 | 2 | 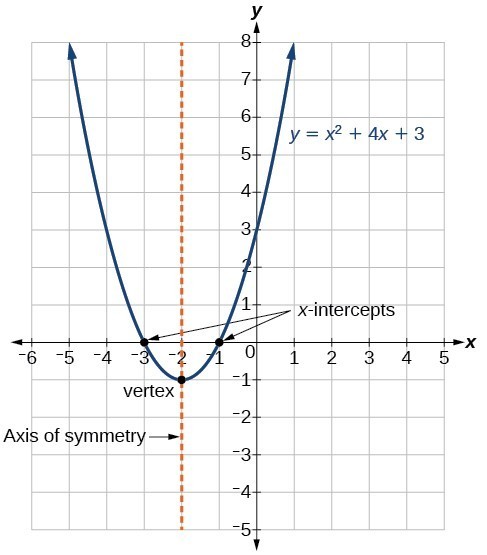 2 |
 2 | 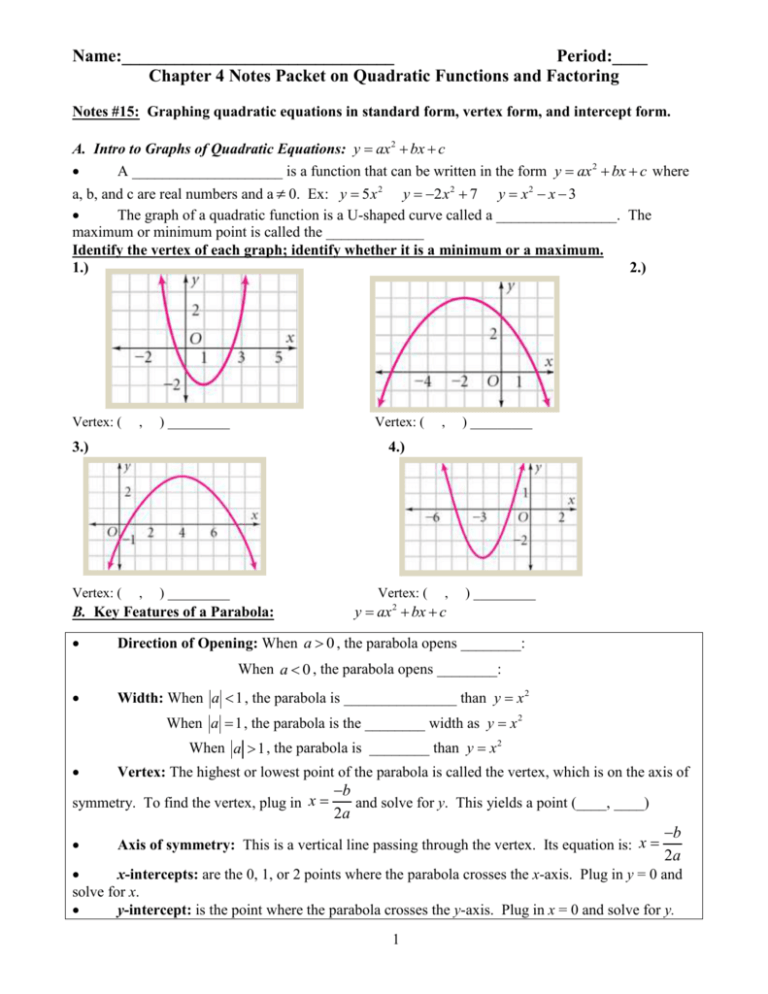 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 2 |  2 |
2 |  2 |  2 |
 2 | 2 | 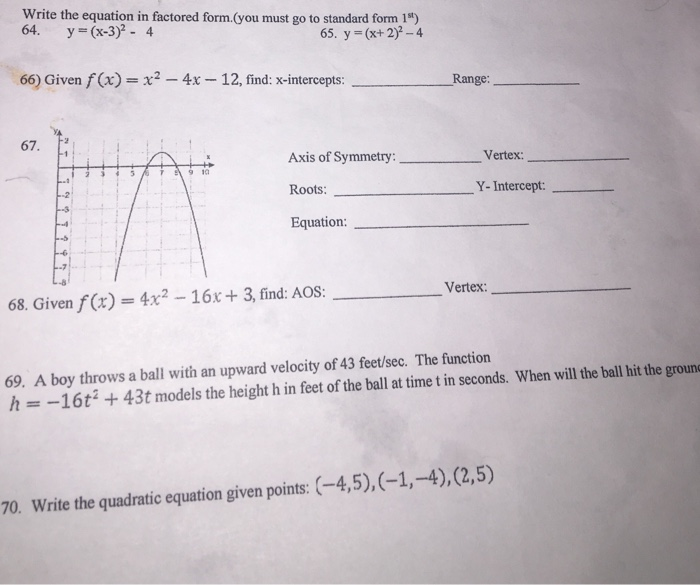 2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |  2 |
2 |  2 | 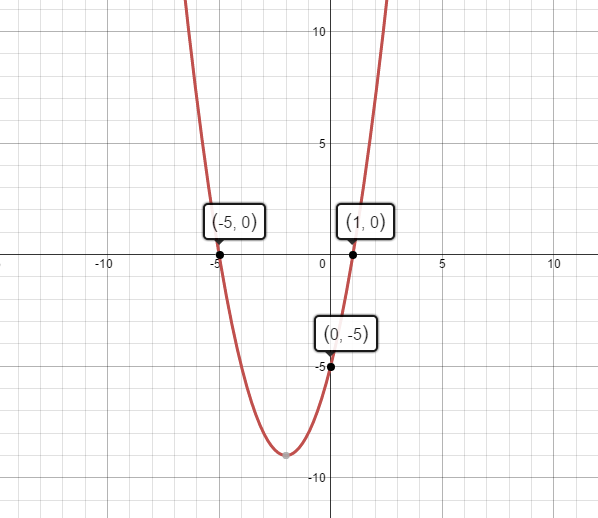 2 |
2 | 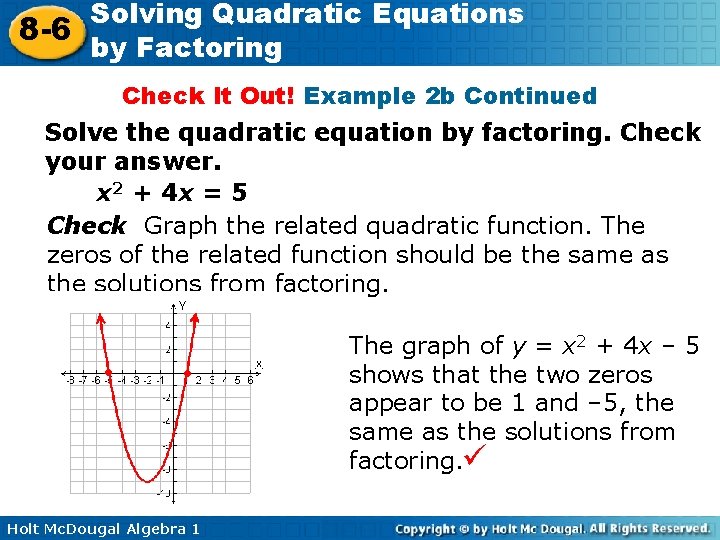 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 2 | 2 |
 2 |  2 |  2 |
2 |  2 | 2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |  2 |
 2 |  2 | 2 |
 2 | 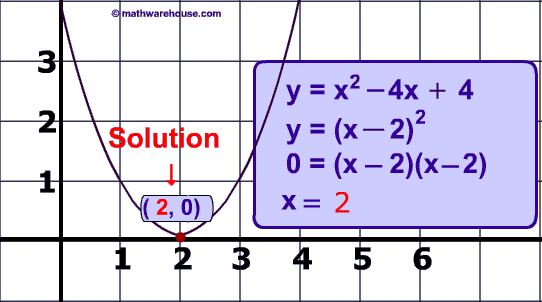 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
2 |  2 |  2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
2 | 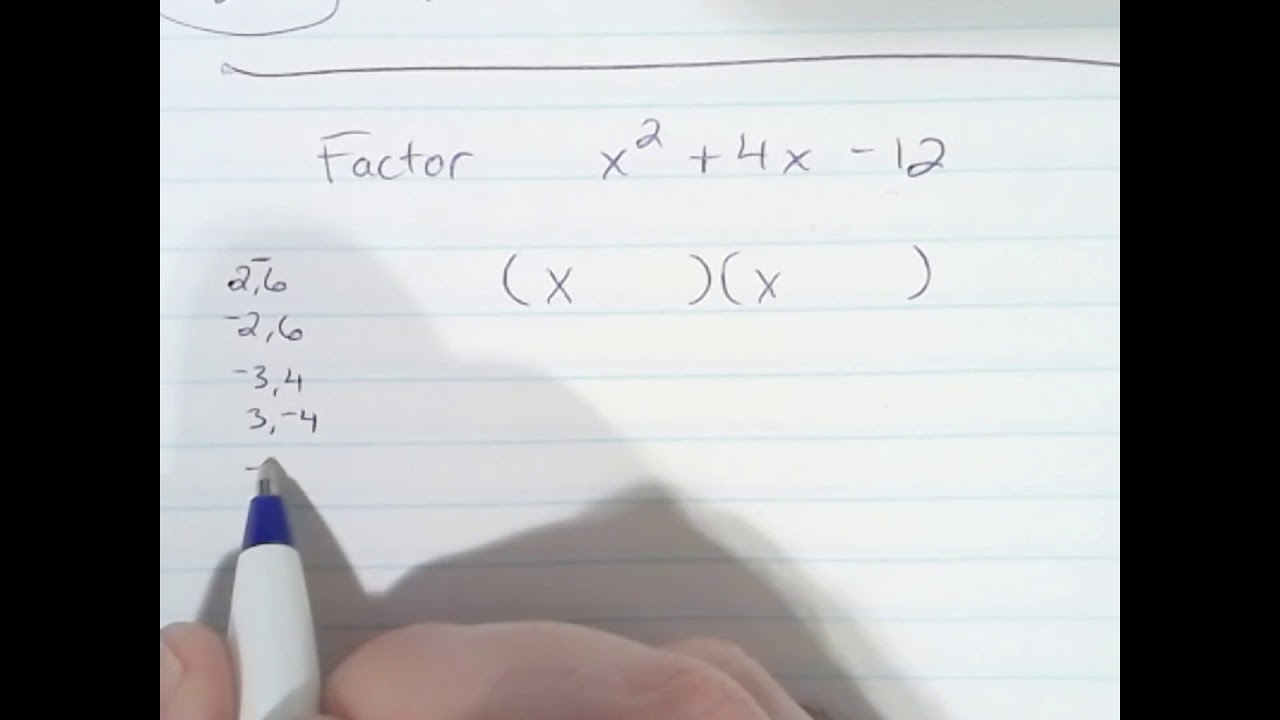 2 |  2 |
 2 | 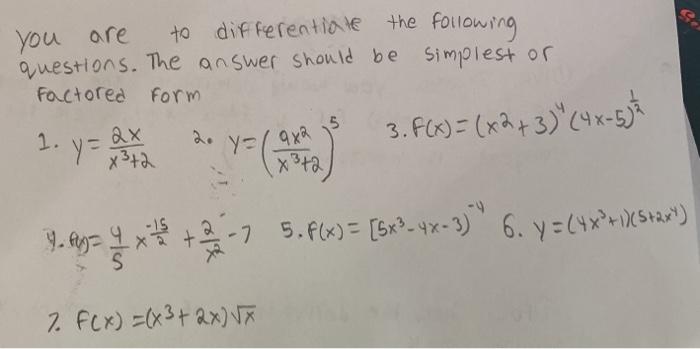 2 |  2 |
2 | 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 | 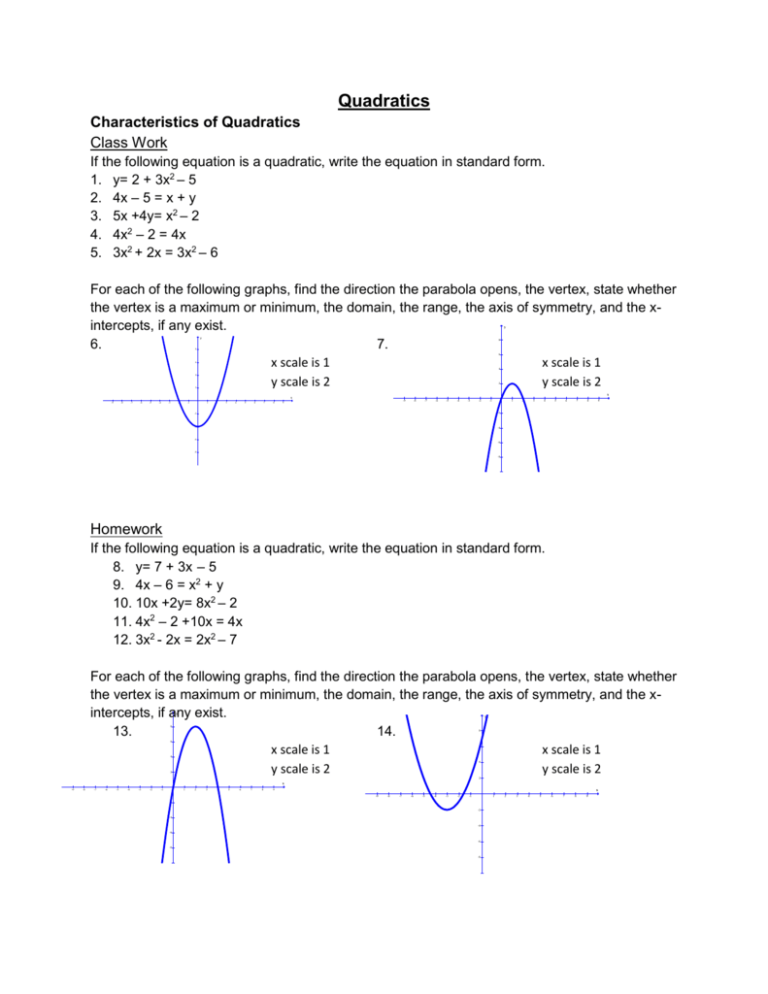 2 |  2 |
 2 |  2 |  2 |
2 | 2 |  2 |
「Y=x^2-4x-5 in factored form」の画像ギャラリー、詳細は各画像をクリックしてください。
 2 |  2 |
As a user of both Algebrator and 30 I have to say that the difference is incredible I found the old Algebrator useful, but it was really difficult to enter more complex expression With your new WYSIWYG interface that problem has been completely What is the factored form of this expression?





0 件のコメント:
コメントを投稿